Highlights
Imperfections could massively improve quantum hard drives: paper in Physical Review Letters
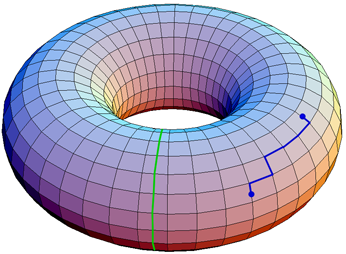
Making quantum bits interact as if they were arranged over the surface of a torus is one idea to build a quantum memory that resists errors. Recent research predicts imperfections would lend such a memory even more resilience.
The last thing you'd expect to be useful in a computer's hard drive is structural flaws, but Research Fellow Alastair Kay of CQT and the University of Oxford, UK, has quantified how imperfections in a quantum hard drive could help solve one of quantum computing's big challenges: protecting delicate quantum data from accumulating errors caused by imperfect operations or interactions with the environment. The result is published in Physical Review Letters.
Classical computer hard drives store information safely for long times without any power. Searching for a comparable way to achieve passive, stable quantum data storage has previously led researchers to propose systems for encoding quantum data known as "toric codes". Alastair derives bounds on how long data is protected in such a system — and shows that the data lifetime is massively extended when the system contains random imperfections.
Toric codes describe a particular way of structuring the interactions between information-storing elements of a quantum hard drive, connecting the quantum bits (qubits) as if they were distributed over the surface of a torus. Data is stored in the global properties of groups of qubits rather than individual qubits, such that single isolated errors cannot destroy it directly. Unfortunately, localised errors can grow into logical errors through the intrinsic interactions of the system, causing the memory to fail.
Alastair considers a two-dimensional toric code subject to a magnetic field, which is the sort of external disruption that can corrupt quantum data in real-life situations. He first shows that the time until there is a more than 50 per cent chance of a logical error having appeared in a system of N quantum bits (qubits) scales as log(N), backing up the theoretical analysis with simulations of a 3-million-qubit toric code.
Can the logical errors be staved off longer? In condensed matter systems, the presence of impurities often curtails dynamical properties such as electrical and thermal conduction, a phenomenon known as Anderson localisation. Alastair explores the recent idea that Anderson localisation can be exploited to control error propagation in a quantum memory implementing a toric code (proposed earlier this year in two papers), quantifying for the first time the expected scale of the improvement in memories of finite size. He calculates that inducing Anderson localisation would (almost always) give an exponential increase in the quantum data storage time – from scaling as log(N) to scaling as N^c (c being some constant). The localisation could be induced by adding random flaws to the structure of the quantum hard drive.

"For the Anderson localisation case, I can't actually do numerics for long enough to get any estimate of when the memory starts destabilising! That's how impressive the technique is," says Alastair (pictured right).
Mathematically, the result is derived by mapping the two-dimensional memory system into an exactly solvable one-dimensional Ising model. The calculations then use Lieb–Robinson bounds, which describe an 'effective speed of light' for the model, to place lower bounds on the relevant dynamical properties.
Two-dimensional toric codes are known not to be good memories except, unrealistically, at absolute zero temperature. However, Alastair hopes his theoretical approach can be extended to prove a set of sufficient conditions that any model will be a good memory.
For more details, see the paper "The Capabilities of a Perturbed Toric Code as a Quantum Memory", Phys. Rev. Lett. 107, 270502 (2012); arXiv:1107.3940.






