Highlights
QIP=PSPACE=IP
Computational Complexity Theory studies how difficult it is to solve a problem, or how hard it is to verify that a proposed solution is indeed correct. The degree of difficulty depends of course on the resources one can use: in particular, quantum physics being more general than classical physics, one might expect the use of quantum resources to help.
However, Rahul Jain of CQT, in collaboration with other researchers, has proved that, in some important scenarios, quantum physics does not help. This is a major results in mathematical sciences.
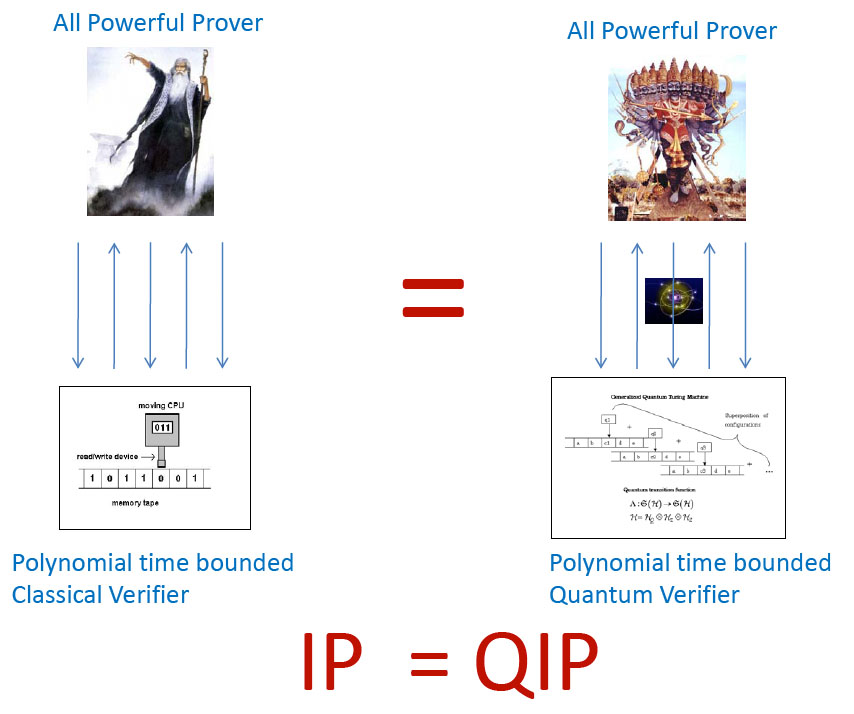
"Interactive proofs" are objects of fundamental significance in Computational Complexity Theory and are different from the "static proofs" as they exist in conventional Mathematics. In an Interactive Proof "an all powerful Prover" tries to convince an efficient "polynomial time bounded Verifier" of correctness of a claim using interaction between them. As with any proof system, Interactive Proofs are required to be "complete", that is true statements have valid proofs, and "sound" that is false statements cannot be proven. The class of problems having Interactive Proofs is denoted IP. The well known complexity class NP can be captured by a one message Interactive Proof with deterministic Verifier, and hence NP is contained in IP. The "P v/s NP" question, which is arguably one of the biggest mysteries of modern times, at a philosophical level asks if it is easier to verify proofs than to come up with them ?
After the complexity class IP was conceived, it was natural to ask how powerful it is ? After a sequence of surprising results it was discovered that IP = PSPACE, the latter being the class of problem that can be solved using polynomial space. In other words, the problems whose proofs can be efficiently verified in time, are precisely the problems that can actually be efficiently solved in space. This was how "time" equated with "space" in the Complexity Theory World.
About a decade ago the quantum analogue of IP, known as QIP was considered, in which the Verifier is a polynomial time bounded quantum machine and the Prover and the Verifier can exchange quantum messages between them. It is easily seen that IP is contained in QIP, since a classical verifier is also a quantum verifier. It was an open question from then on to understand the power of QIP more precisely, specifically in comparison to PSPACE. We (Jain, Ji, Upadhyah, Watrous) settle this long standing question and show that QIP is also contained in PSPACE and hence QIP = PSPACE = IP. This unfortunately shows that Quantum Interactive Proofs do not have extra power over Classical Interactive Proofs, such is the world, we got to live in it ! Also in other words, "quantum verification efficiently in time" equates "classical solution efficiently in space".
One of the main techniques used to obtain this result is to exhibit fast parallel algorithms for solving a certain class of semi-definite programs that capture the expressive power of Quantum Interactive Proofs. Fast parallel algorithms for semi-definite programs appear to be a powerful tool with possibly other interesting consequences as well.
Written by: Rahul Jain, Centre for Quantum Technologies






